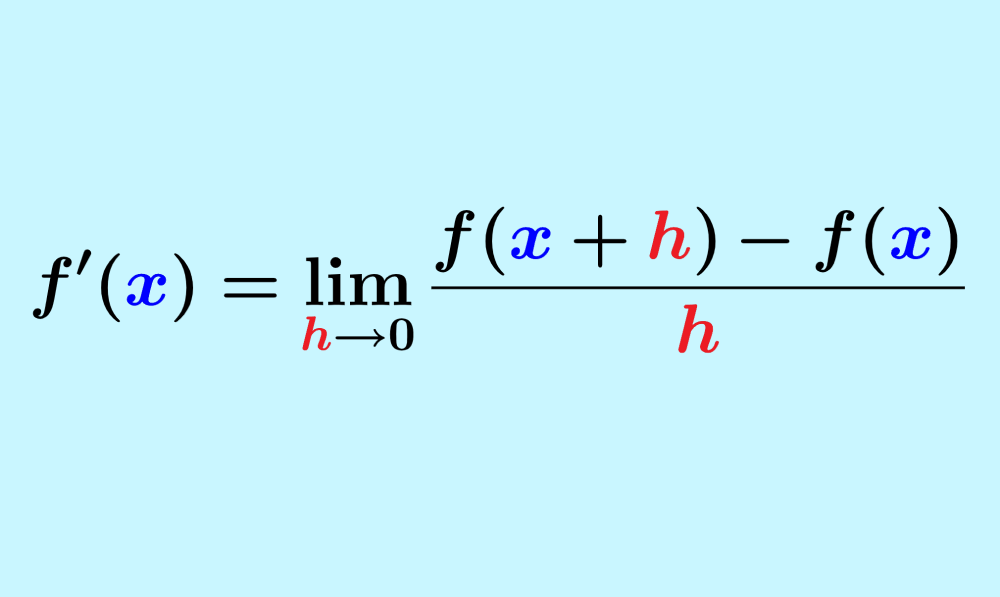A definição da derivada como limite pode ser encontrada usando a fórmula do declive para encontrar o declive da reta secante entre dois pontos da função. Em seguida, usamos um limite para aproximar os pontos, de modo que o declive da secante seja uma aproximação do declive da tangente.
A seguir, aprenderemos sobre a definição da derivada como limite. Usaremos um diagrama para encontrar essa definição passo a passo. Depois, vamos aplicar essa ideia para calcular algumas derivadas.
Como definir a derivada usando limites
Vamos usar limites para encontrar uma equação que nos permita obter o declive da reta tangente a uma função. Para isso utilizamos o seguinte diagrama:
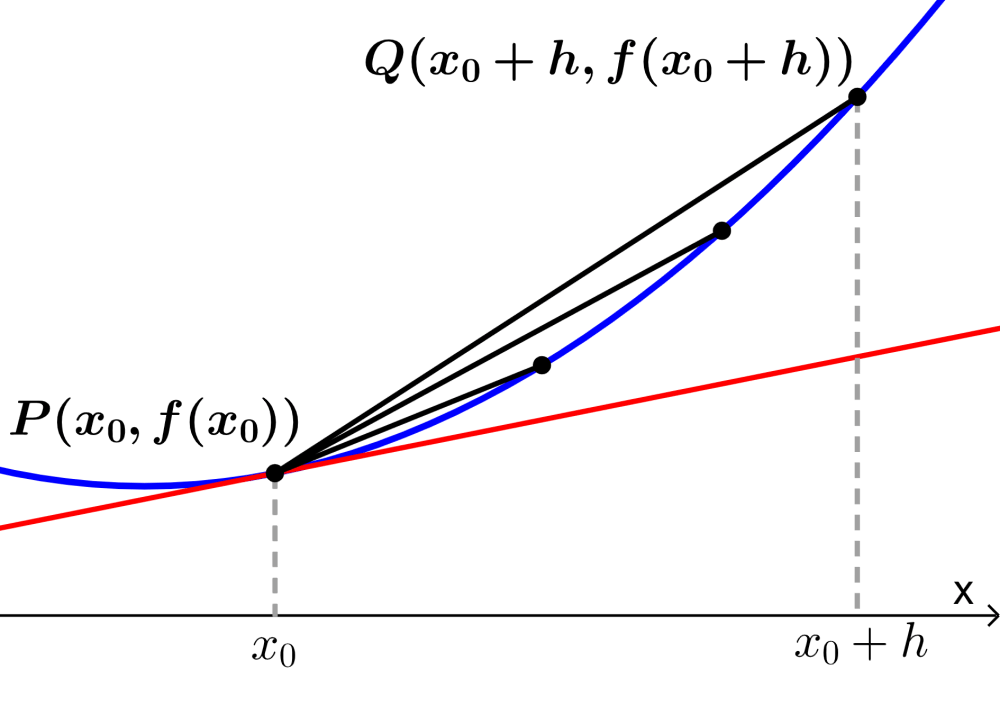
Considere o ponto $latex P~(x_{0},~ f(x_{0}))$ que se encontra na curva produzida pela função $latex f(x)$, conforme mostrado no diagrama. Vamos encontrar o declive da reta tangente a f no ponto P.
Podemos encontrar o declive usando o ponto $latex Q~(x_{0}+h,~f(x_{0}+h)$, que é h unidades de P e assumimos que h é muito pequeno.
Então, começamos calculando o declive da reta secante PQ. Sabemos que o declive é igual à variação de y sobre a variação de x. Então temos:
$$\text{Inclinação PQ}=\frac{f(x_{0}+h)-f(x_{0})}{x_{0}+h-x_{0}}$$
$$\text{Inclinação PQ}=\frac{f(x_{0}+h)-f(x_{0})}{h}$$
Se h for suficientemente pequeno, o ponto Q se aproximará cada vez mais de P até que o declive da reta secante PQ seja uma boa aproximação para o declive da reta tangente em P.
Assim, definimos o declive da reta tangente como o limite do declive da reta secante quando h se aproxima de 0:
$$m_{tan}=\lim _{h \to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}$$
Agora, em vez de usar a constante $latex x_{0}$, podemos usar a variável $latex x$. Assim, o limite resultante será uma expressão em termos de x.
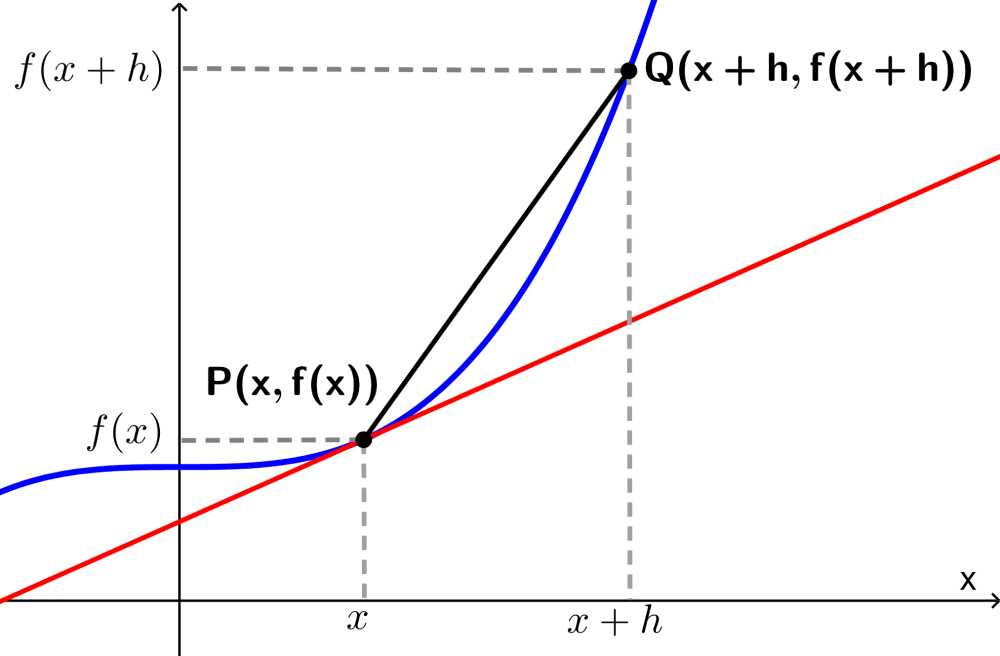
Esta expressão pode ser considerada como uma função de x. Além disso, esta função, que pode ser denotada por $latex f'(x)$, é a derivada da função f.
Então, se temos que $latex f(x)$ é uma função de x, a derivada de f em x é:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Derivada de uma função como uma taxa de variação
A derivada de uma função $latex f(x)$ em x é a taxa de variação instantânea da função em x. Isso ocorre por a derivada ser definida como o limite, que encontra o declive da reta tangente a uma função.
Lembre-se de que o declive representa a mudança em y sobre a mudança em x. Ou seja, temos uma taxa de variação em relação a x.
Se $latex y=f(x)$ é uma função de x, então também podemos usar a notação $latex \frac{dy}{dx}$ para representar a derivada de f.
$latex \frac{dy}{dx}$ é a derivada de y em relação a x. Ou seja, essa é a taxa na qual y muda quando x muda.
Por exemplo, se $latex d(t)$ representa o deslocamento de um carro no tempo t, então $latex d'(t)$ representa a velocidade do carro no tempo t. Se $latex y=f(x)$ é uma função de x, então $latex f'(x)$ representa como y muda quando x muda.
Se $latex f'(x)$ é positivo em um certo ponto, então y aumenta à medida que x aumenta. Se $latex f'(x)$ for negativo em algum ponto, então y diminui à medida que x aumenta.
Exemplos de derivadas usando limites
A seguir estão alguns exemplos de como encontrar a derivada de uma função usando sua definição como limites.
EXEMPLO 1
Encontre a derivada de $latex f(x)=10x$ usando a definição de derivada por limites.
Solução: Uma derivada pode ser encontrada usando a seguinte fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Então, usamos a função $latex f(x)=10x$ no numerador e temos:
$$f'(x)=\lim _{h \to 0}\frac{10(x+h)-10x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{10x+10h-10x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{10h}{h}$$
Simplificando o h no numerador com o h no denominador, temos:
$$f'(x)=\lim _{h \to 0}(10)$$
Como não temos nenhum h, simplesmente removemos o limite:
$latex f'(x)=10$
EXEMPLO 2
Encontre a derivada de $latex f(x)=3x^2$ usando a definição da derivada com limites.
Solução: Usamos a fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Então, reescrevemos o numerador usando $latex f(x)=3x^2$ e temos:
$$f'(x)=\lim _{h \to 0}\frac{3(x+h)^2-3x^2}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{3x^2+6hx+3h^2-3x^2}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{6hx+3h^2}{h}$$
Podemos fatorar o h do numerador e simplificar com o denominador:
$$f'(x)=\lim _{h \to 0}\frac{h(6x+3h)}{h}$$
$$f'(x)=\lim _{h \to 0}(6x+3h)$$
Finalmente, resolvemos o limite substituindo $latex h=0$ na expressão:
$latex f'(x)=6x+3(0)$
$latex f'(x)=6x$
EXEMPLO 3
Encontre a derivada de $latex f(x)=5x^2+6x$ usando limites.
Solução: A fórmula para a derivada de uma função usando limites é:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Então, usando a função $latex f(x)=5x^2+6x$ no numerador, temos:
$$f'(x)=\lim _{h \to 0}\frac{(5(x+h)^2+6(x+h))-(5x^2+6x)}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{5(x^2+2hx+h^2)+6x+6h-5x^2-6x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{5x^2+10hx+5h^2+6x+6h-5x^2-6x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{10hx+5h^2+6h}{h}$$
Fatoramos o h do numerador para simplificar com o h do denominador:
$$f'(x)=\lim _{h \to 0}\frac{h(10x+5h+6)}{h}$$
$$f'(x)=\lim _{h \to 0}(10x+5h+6)$$
Finalmente, resolvemos o limite substituindo $latex h=0$ na expressão:
$latex f'(x)=10x+5(0)+6$
$latex f'(x)=10x+6$
Veja também
Interessado em aprender mais sobre derivadas de funções? Você pode olhar para estas páginas: