Antes de efetuar a redução ao 1° quadrante é interessante determinar a primeira determinação positiva do ângulo.
sen (360° · k + θ) = senθ, k ∈ ℤ
cos (360° · k + θ) = cosθ, k ∈ ℤ
tg (360° · k + θ)= tgθ, k ∈ ℤ
sen (2π · k + θ) = senθ, k ∈ ℤ
cos (2π · k + θ) = cosθ, k ∈ ℤ
tg (2π · k + θ) = tgθ, k ∈ ℤ
Dessa forma, ao efetuarmos a redução ao 1º quadrante, vamos relacionar sempre ângulos na primeira volta.
A figura a seguir representa um ciclo trigonométrico no qual foi marcada a imagem P do ângulo θ∈ [0, π/2].
Os pontos P2, P3 e P4 são simétricos do ponto P em relação ao eixo Oy, à origem e ao eixo Ox, respectivamente. Assim, o quadrilátero PP2P3P4 é um retângulo e AÔP =A’O̲P̲^2 = A’O̲P̲^3 = AOQP4= θ.
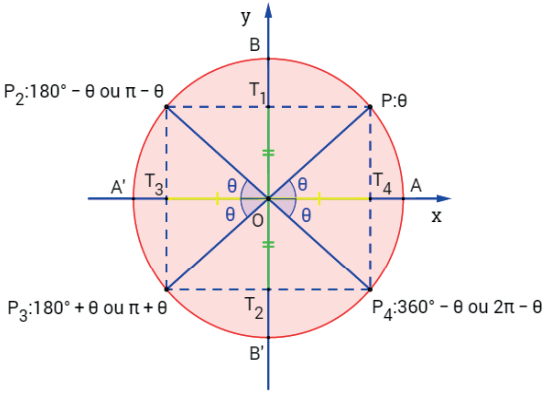
O arco de imagem P2 na primeira volta é 180°- θ ou π – θ.
O arco de imagem P3 na primeira volta é 180°+ θ ou π + θ.
O arco de imagem P4 na primeira volta é 360° – θ ou 2π – θ.
Observe que, a menos do sinal, os arcos de imagem P1P2′,P3 e P4 têm as mesmas linhas trigonométricas, pois |OT1| = |OT2| e |OT3| = |OT4|.
Analisando o sinal das linhas trigonométricas em cada um dos quadrantes, podemos concluir que:
sen θ = sen (π – θ) =- sen (π + θ) =- sen(2π – θ) ou
sen θ = sen (180°- θ) = -sen (180° + θ) =-sen (360°-θ)
cos θ = – cos (π – θ) = -cos(π + θ) = cos(2π – θ) ou
cos θ = – cos (180° – θ) = -cos (180° + θ) = cos (360° – θ)
tg θ =-tg (π – θ) = tg (π + θ) =-tg(2π – θ) ou
tg θ = -tg (180° – θ) = tg (180° + θ) =-tg (360° – θ)
Para efetuar a redução ao 1° quadrante, é útil associar o valor da linha trigonométrica de cada um dos ângulos à do ângulo correspondente no 1° quadrante.
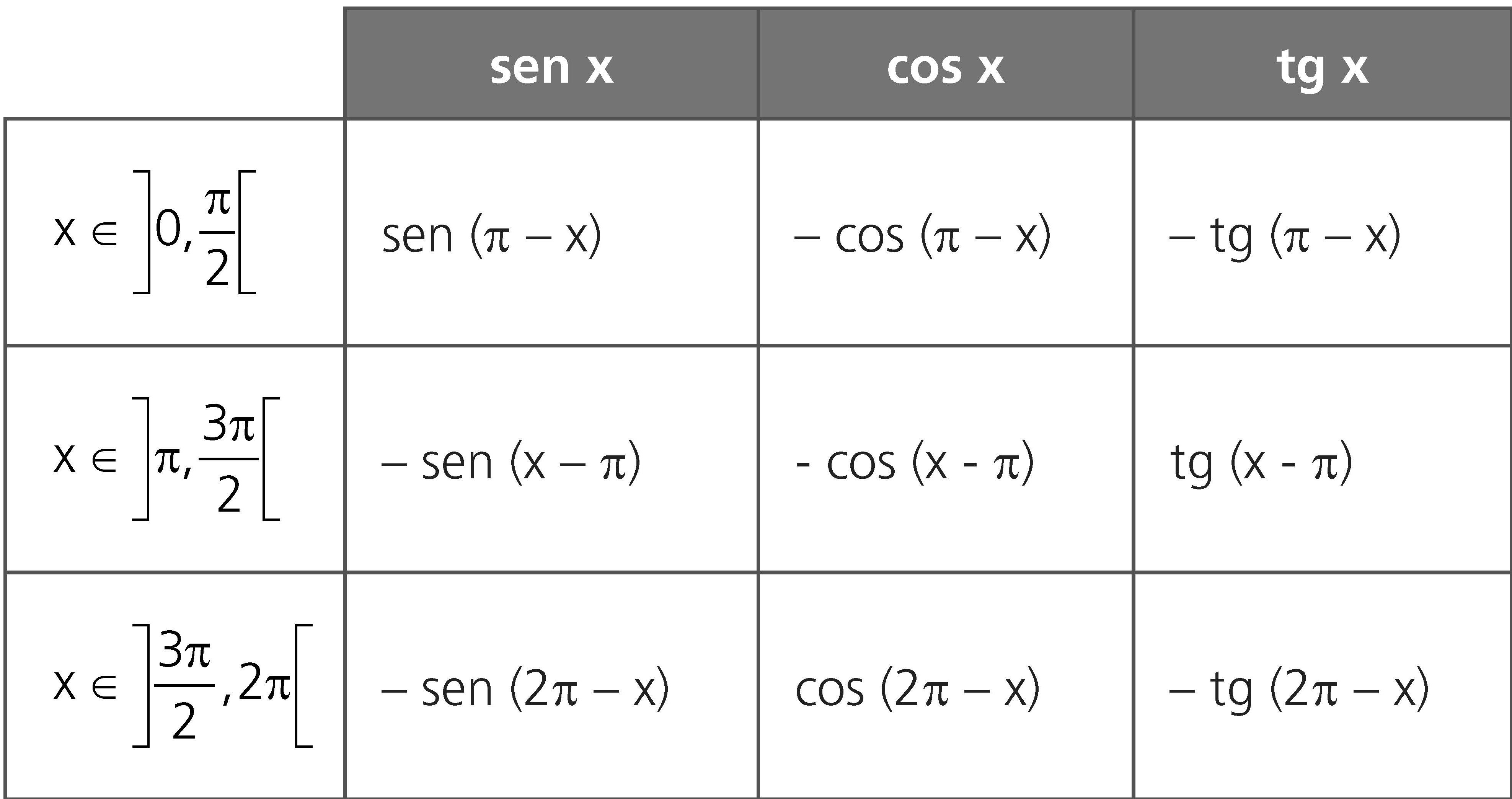
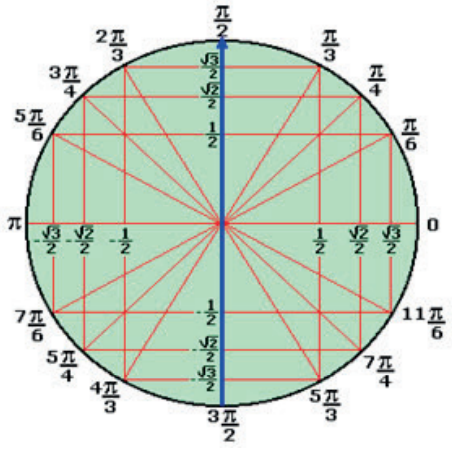
Observe que nessas relações o resultado apresenta sempre a mesma linha trigonométrica com o sinal dela no quadrante de origem. Por exemplo, no 2° quadrante, o seno é positivo, o cosseno e a tangente negativos.
Exemplos:
sen 120° = sen (180° – 60°) = sen60° = √3/2
cos 120° = cos (180° – 60°) =- cos60° =- 1/2
sen 150° = sen (180° – 30°) = sen30° = 1/2
cos 150° = cos (180° – 30°) = -cos30° = – √3/2
sen 315° = sen (360° – 45°) = -sen45° =- √2/2
cos 315° = cos (360° – 45°) = cos45° = √2/2
Exemplo:
A expressão sen (17π + θ) + sen (18π – θ) + sen (19π – θ) + sen (20π – θ), onde θ é um ângulo do 3° quadrante, vale:
a) senθ
b) -senθ
c) 2 senθ
d) -2 senθ
e) 0
Resolução: E
sen (17π + θ) = sen (2π · 8 + π + θ)= sen (π + θ) = -senθ
sen (18π – θ) = sen (2π · 8 + 2π – θ) = sen (2π – θ) =-senθ
sen (19π – θ) = sen (2π · 9 + π – θ) = sen (π – θ)= senθ
sen (20π + θ) = sen (2π · 10 + θ) = senθ
sen (17π + θ) +sen(18π – θ) + sen (sen19π – θ) + sen (20π + θ) = (-senθ) + (-senθ) + senθ + senθ = 0
Observe que o quadrante do ângulo θθ não afeta em nada a utilização das relações de redução ao 1° quadrante.





