Le proporzioni
Classe
2a
della scuola media
Matematica utile
Le proporzioni ci servono per risolvere alcuni problemi nei
quali conosciamo tre grandezze, cioè tre numeri, e ci manca un quarto numero che
non conosciamo e che vogliamo calcolare.
 |
|
due frazioni
uguali |
Per fare una proporzione servono due frazioni uguali come
rapporto, cioè come risultato o come quoziente.
Esempio
4:2 = 2
Se calcolo quattro diviso due, ottengo come risultato 2.
8:4 = 2
Se calcolo otto diviso quattro, ottengo come risultato sempre 2.
 |
|
la
proporzione |
Unisco le due frazioni uguali e le scrivo in questo modo:
4:2=8:4
Se scrivo in questo modo ho scritto una eguaglianza, in quanto
ho messo il simbolo di = (uguale) al centro; questa eguaglianza si chiama
proporzione.
Il vantaggio si ha in alcuni problemi in cui si conoscono tre
numeri ma manca il quarto.
Esempio
Trova il numero che non conosco e che indico con la lettera x
(ics), da non confondere con il per.
x:2=8:4
Soluzione
Se mi ricordo una proporzione, tipo questa:
4:2=8:4
posso dire subito che il numero nascosto, cioè non conosciuto o
incognito è il numero 4.
Quindi scrivo:
x=4
Ci serve, ora, una regola che vale sempre, per cui occorre
dare dei nomi agli elementi di ogni proporzione.
 |
|
la
proporzione |
Si chiama antecedente il numero che si trova prima del simbolo
della divisione, cioè prima di : (due punti).
Se scrivo:
4:2
l'antecedente è 4, perché si trova prima del diviso.
Se scrivo:
8:4
l'antecedente è 8, perché si trova prima del diviso.
Si chiama conseguente il numero che si trova dopo la divisione.
Se scrivo:
4:2
il conseguente è 2, perché si trova dopo la divisione.
Se scrivo:
8:4
il conseguente è 4, perché si trova dopo la divisione.
Consideriamo ora la seguente proporzione:
4:2=6:3
Si legge:quattro sta a due come sei sta a tre.
 |
|
la proporzione |
Oltre a precedente e conseguente, occorre distinguere i quattro
numeri della proporzione in base alla posizione in cui si trovano. La parola
estremo significa che si trova quasi all'esterno, cioè lontano dal centro.
Consideriamo ora la seguente proporzione:
4:2=6:3
Gli estremi della proporzione sono i numeri 4 e 3; essi infatti
si trovano sull'inizio della proporzione, cioè il 4; mentre il 3 si trova sulla
fine della proporzione.
I due numeri che stanno al centro si chiamano medi, cioè stanno
nel mezzo, nel centro della proporzione.
Consideriamo ora la seguente proporzione:
4:2=6:3
I medi della proporzione sono i numeri 2 e 6; essi infatti si
trovano nel centro, vicini al simbolo di eguaglianza, cioè di = (uguale).
Questi nomi ci servono per scrivere le regole di una
proporzione; esse valgono per ogni proporzione.
Proprietà fondamentale
In ogni proporzione il prodotto dei medi è uguale al prodotto
degli estremi.
Vediamo se è vera questa prima proprietà.
Consideriamo la seguente proporzione:
4:2=6:3
Gli estremi della proporzione sono i numeri 4 e 3;
Eseguo la moltiplicazione:
4
·
3 = 12
Al posto di mettere il per con la lettera x è meglio
mettere un punto al centro, per distinguerlo dalla lettera sconosciuta, detta
incognita.
Consideriamo la seguente proporzione:
4:2=6:3
I medi della proporzione sono i numeri 2 e 6;
2
· 6 = 12
La prima proprietà è vera. Proviamo con un'altra proporzione.
4:2=8:4
I medi sono 2 e 8; ho:
2
· 8 = 16
Gli estremi sono 4 e 4; ho:
4
· 4 = 16
La prima proprietà è vera anche per questa proporzione.
Ripetiamo, quindi, che la proprietà fondamentale delle
proporzioni è:
In ogni proporzione il prodotto dei medi è uguale al prodotto
degli estremi.
Questa proprietà fondamentale ci serve per risolvere alcuni
problemi.
Esempio
Data la proporzione:
4:2=6:x
trovare il valore della incognita x.
Soluzione
Sappiamo già che x=3, ma dobbiamo sfruttare la prima proprietà
fondamentale delle proporzioni, cioè:
In ogni proporzione il prodotto dei medi è uguale al prodotto
degli estremi.
Considero la proporzione:
4:2=6:x
i medi sono 2 e 6; ho:
2
· 6 = 12
Gli estremi sono 4 e x; ho:
4
· x = 12
essendo il prodotto dei medi uguale al prodotto degli estremi;
per trovare la x, divido per 4 primo e secondo membro ed ottengo:

Quindi x=3 come sapevamo già.
Esempio
Data la proporzione:
4:x=6:3
trovare il valore della incognita x.
Soluzione
Sappiamo già che x=2, ma dobbiamo sfruttare la prima proprietà
fondamentale delle proporzioni, cioè:
In ogni proporzione il prodotto dei medi è uguale al prodotto
degli estremi.
Considero la proporzione:
4:x=6:3
Gli estremi sono 4 e 3; ho:
4
· 3 = 12
I medi sono x e 6; ho:
6
· x = 12
essendo il prodotto dei medi uguale al prodotto degli estremi;
per trovare la x, divido per 6 primo e secondo membro ed ottengo:

Quindi x=2 come sapevamo già.
Consideriamo ora la seguente proporzione:
9:x=x:4
Gli estremi della proporzione sono 9 e 4;
ho:
9
· 4 = 36
I medi sono x e x; ho:
x
· x = 36 cioè:
x2=36
Eseguo la radice quadrata del primo e del secondo membro ed
ottengo:
x=6
La proporzione è quindi:
9:6=6:4
Una proporzione in cui i due medi sono costituiti dallo stesso
numero si dice proporzione continua; e il numero medio si chiama medio
proporzionale della proporzione. Il medio proporzionale viene usato anche nei
teoremi di Euclide.
In un triangolo rettangolo un cateto è medio proporzionale tra
l'ipotenusa e la proiezione del cateto stesso sull'ipotenusa. Questo è il primo
Teorema di Euclide.
Il secondo Teorema di Euclide dice:
In un triangolo rettangolo l'altezza relativa all'ipotenusa è
medio proporzionale tra le proiezioni dei due cateti sull'ipotenusa.
Esempio
In un triangolo rettangolo le
proiezioni dei cateti sull'ipotenusa sono rispettivamente 9 cm e 16 cm. Calcola
l'altezza relativa all'ipotenusa.
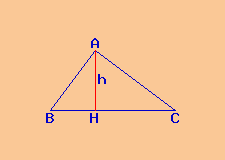
Dati
Poligono: triangolo rettangolo BCA
proiezione BH del cateto AB su ipotenusa = 9 cm
proiezione HC del cateto AC su ipotenusa = 16 cm
Soluzione
Si richiede segmento AH = altezza h relativa all'ipotenusa di un triangolo
rettangolo BCA avente:
proiezione BH del cateto AB su ipotenusa = 9 cm
proiezione HC del cateto AC su ipotenusa = 16 cm
Applico la formula derivata dal 2° Teorema di Euclide che dice:
L'altezza relativa all'ipotenusa è medio proporzionale tra le proiezioni dei
due cateti sull'ipotenusa.
ed ottengo:
altezza h relativa all'ipotenusa =
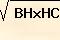 =
=
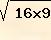 = 12 cm
= 12 cm
Risposta
L'altezza h relativa all'ipotenusa del triangolo rettangolo ABC è: h = 12 cm.
Esempio
In un triangolo rettangolo
l'ipotenusa misura 25 cm e la proiezione di un cateto sull'ipotenusa è di 9 cm.
Calcola i due cateti.
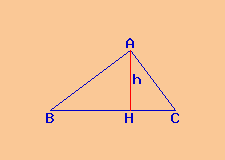
Dati
Poligono: triangolo rettangolo BCA
ipotenusa a = 25 cm
proiezione cateto b su ipotenusa = 9 cm
Soluzione
Si richiede un cateto di un triangolo rettangolo BCA avente:
proiezione HC del cateto b su ipotenusa = 9 cm
ipotenusa a = BC = 25 cm
Applico la formula derivata dal 1° Teorema di Euclide:
cateto b = AC = V a x HC ed
ottengo:
b = V25 x 9 = 15 cm
Mi calcolo la proiezione BH del cateto c su ipotenusa con la formula:
BH = BC - HC = 25 - 9 = 16 cm
Per il cateto c = BA applico la formula derivata dal 1° Teorema di Euclide che
dice:
Un cateto è medio proporzionale tra l'ipotenusa e la proiezione del cateto
stesso sull'ipotenusa.
ed ottengo:
cateto c = BA = V a x BH ed
ottengo:
c = V25 x 16 = 20 cm
Risposta
Un cateto del triangolo rettangolo BCA è b = 15 cm.
L'altro cateto del triangolo rettangolo BCA è c = 20 cm.
prof.
Pietro
De Paolis
Esercizi
da svolgere
Corso di matematica per scuola media
Geometria e artimetica per scuola media
Indice Scuola Elettrica - ridotto a 90




Scuola
Elettrica
Altre applicazioni
Mappa per tipo di scuola
Indice di tutte le pagine del
sito
Guida per navigare
Richiesta informazioni
Scuola
Elettrica





















