Nella regressione di Poisson ci sono due deviazioni.

La Devianza nulla mostra quanto bene la variabile di risposta è prevista da un modello che include solo l'intercetta (media generale).

E la Devianza residua è −2 volte la differenza tra la log-verosimiglianza valutata alla stima di massima verosimiglianza (MLE) e la log-verosimiglianza per un "modello saturo" (un modello teorico con un parametro separato per ogni osservazione e quindi un adattamento perfetto).

Ora annotiamo quelle funzioni di probabilità.

Supponiamo che $ Y $ abbia una distribuzione di Poisson la cui media dipende dal vettore $ \ bf {x} $, per semplicità supporremo che $ \ bf {x} $ abbia solo una variabile predittore. Scriviamo $$ E (Y | x) = \ lambda (x) $$ Per la regressione di Poisson possiamo scegliere un log o una funzione di collegamento identità, scegliamo un link di log qui.

$$ Log (\ lambda (x)) = \ beta_0 + \ beta_1x $$

$ \ beta_0 $ è l'intercetta.

La funzione Likelihood con il parametro $ \ beta_0 $ e $ \ beta_1 $ è $$ L (\ beta_0, \ beta_1; y_i) = \ prod_ {i = 1} ^ {n} \ frac {e ^ {- \ lambda {(x_i)}} [\ lambda (x_i)] ^ {y_i}} { y_i!} = \ prod_ {i = 1} ^ {n} \ frac {e ^ {- e ^ {(\ beta_0 + \ beta_1x_i)}} \ left [e ^ {(\ beta_0 + \ beta_1x_i)} \ right] ^ {y_i}} {y_i!} $$ La funzione di probabilità del registro è:

$$ l (\ beta_0, \ beta_1; y_i) = - \ sum_ {i = 1} ^ ne ^ {(\ beta_0 + \ beta_1x_i)} + \ sum_ {i = 1} ^ ny_i (\ beta_0 + \ beta_1x_i) - \ sum_ { i = 1} ^ n \ log (y_i!) \ tag {1} $$ Quando calcoliamo null deviance inseriremo $ \ beta_0 $ in $ (1) $. $ \ beta_0 $ sarà calcolato da una regressione di sola intercettazione, $ \ beta_1 $ sarà impostato a zero. Scriviamo $$ l (\ beta_0; y_i) = - \ sum_ {i = 1} ^ ne ^ {\ beta_0} + \ sum_ {i = 1} ^ ny_i \ beta_0- \ sum_ {i = 1} ^ n \ log (y_i! ) \ tag {2} $$ Successivamente dobbiamo calcolare la probabilità logaritmica per il "modello saturato" (un modello teorico con un parametro separato per ogni osservazione), quindi abbiamo i parametri $ \ mu_1, \ mu_2, ..., \ mu_n $ qui.

(Nota, in $ (1) $, abbiamo solo due parametri, ovvero finché il soggetto ha lo stesso valore per le variabili predittore, pensiamo che siano le stesse).

La funzione di verosimiglianza per "modello saturo" è $$ l (\ mu) = \ sum_ {i = 1} ^ n y_i \ log \ mu_i- \ sum_ {i = 1} ^ n \ mu_i- \ sum_ {i = 1} ^ n \ log (y_i!) $$ Quindi può essere scritto come: $$ l (\ mu) = \ sum y_i I _ {(y_i>0)} \ log \ mu_i- \ sum \ mu_iI _ {(y_i>0)} - \ sum \ log (y_i!) I _ {(y_i>0)} - \ sum \ mu_iI_ (y_i = 0)} \ tag {3} $$ (Nota, $ y_i \ ge 0 $, quando $ y_i = 0, y_i \ log \ mu_i = 0 $ e $ \ log (y_i!) = 0 $, sarà utile in seguito, non ora) $$ \ frac {\ partial} {\ partial \ mu_i} l (\ mu) = \ frac {y_i} {\ mu_i} -1 $$ impostato a zero, otteniamo

$$ \ hat {\ mu_i} = y_i $$ Ora metti $ \ hat {\ mu_i} $ in $ (3) $, poiché quando $ y_i = 0 $ possiamo vedere che $ \ hat {\ mu_i} $ sarà zero.

Ora per la funzione di verosimiglianza $ (3) $ del "modello saturato" possiamo solo preoccuparci di $ y_i>0 $, scriviamo $$ l (\ hat {\ mu}) = \ sum y_i \ log {y_i} - \ sum y_i- \ sum \ log (y_i!) \ tag {4} $$

Da $ (4) $ puoi capire perché abbiamo bisogno di $ (3) $ poiché $ \ log y_i $ non sarà definito quando $ y_i = 0 $

Adesso calcoliamo le deviazioni.

The Residual Deviance = $$ - 2 [(1) - (4)] = - 2 * [l (\ beta_0, \ beta_1; y_i) -l (\ hat {\ mu})] \ tag {5 } $$

Il Null Deviance = $$ - 2 [(2) - (4)] = - 2 * [l (\ beta_0; y_i) -l (\ hat {\ mu})] \ tag {6} $$

Ok, ora calcoliamo le due deviazioni con R e poi con "mano" o excel.

  x<- c (2,15,19,14,16,15,9,17,10,23,14,14,9,5,17,16,13,6,16,19, 24,9,12,7,9,7,15,21,20,20)
y<-c (0,6,4,1,5,2,2,10,3,10,2,6,5,2,2,7,6,2,5,5,6,2,5, 1,3,3,3,4,6,9)
p_data<-data.frame (y, x)
p_glm<-glm (y ~ x, family = poisson, data = p_data)
riepilogo (p_glm)
 

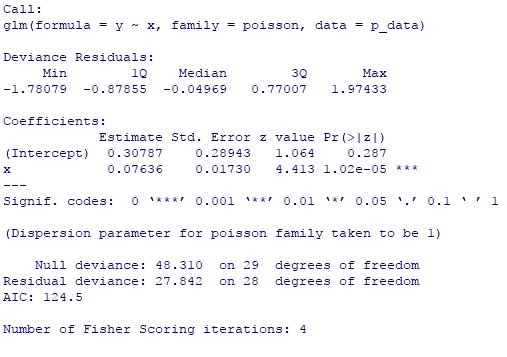
Puoi vedere $ \ beta_0 = 0.30787, \ beta_1 = 0.07636 $, Null Deviance = 48.31, Residual Deviance = 27.84.

Ecco il modello di sola intercettazione

  p_glm2<-glm (y ~ 1, family = poisson, data = p_data)
riepilogo (p_glm2)
 

Puoi vedere $ \ beta_0 = 1.44299 $

Ora calcoliamo queste due deviazioni manualmente (o tramite Excel)

  l_satured<-c ()
l_regression<-c ()
l_intercept<-c ()

per (i in 1:30) {
l_regression [i] < - exp (0.30787 +0.07636 * x [i]) + y [i] * (0.30787 + 0.07636 * x [i]) -
log (fattoriale (y [i]))}

l_reg<-sum (l_regression)
l_reg
# -60.25116 ### log verosimiglianza per il modello di regressione

per (i in 1:30) {
l_saturato [i] <-y [i] * try (log (y [i]), T) -y [i] -log (fattoriale (y [i]))
} # c'è un y_i = 0 che devi fare attenzione
l_sat<-sum (l_satured, na.rm = T)
l_sat
# -46.33012 ### log verosimiglianza per il modello saturo

per (i in 1:30) {
l_intercept [i] < - exp (1.44299) + y2 [i] * (1.44299) -log (fattoriale (y [i]))
}

l_inter<-sum (l_intercept)
l_inter

# -70.48501 ## registra probabilità solo per il modello di intercettazione

-2 * (l_reg-l_sat)

# 27.84209 ## Devianza residua

-2 * (l_inter-l_sat)

## 48.30979 ## Null Deviance
 

Puoi vedere utilizzare queste formule e calcolare a mano puoi ottenere esattamente gli stessi numeri calcolati dalla funzione GLM di R.