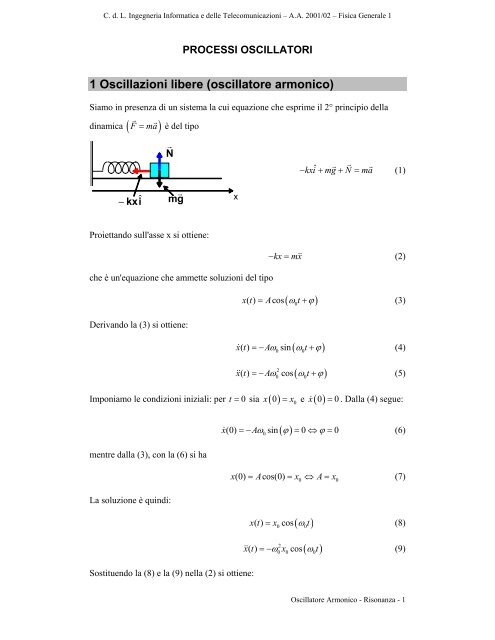
1 Oscillazioni libere (oscillatore armonico) ( ) ( ) ( ) ( ) 0 e ( )0 - Fisica

C. d. L. Ingegneria Informatica e delle Telecomunicazioni – A.A. 2001/02 – Fisica Generale 1 

PROCESSI OSCILLATORI 

1 Oscillazioni libere (oscillatore armonico) 

Siamo in presenza di un sistema la cui equazione che esprime il 2° principio della 

 

F = ma è del tipo 

dinamica ( ) 

− kxi 

 

N 

mg 

Proiettando sull'asse x si ottiene: 

che è un'equazione che ammette soluzioni del tipo 

Derivando la (3) si ottiene: 

Imponiamo le condizioni iniziali: per 0 

mentre dalla (3), con la (6) si ha 

La soluzione è quindi: 

Sostituendo la (8) e la (9) nella (2) si ottiene: 

x 

kxiˆ 

− + mg + N = ma (1) 

− kx = mx (2) 

( ω ϕ ) 

xt () = Acos t+ 

(3) 

0 

0 0 

( ) 

xt () = − Aω sinω 

t+ 

ϕ 

(4) 

2 

0 0 

( ) 

xt () = − Aω cosω 

t+ 

ϕ 

(5) 

t = sia x( 0) 

x0 

0 

= e ( ) 

( ) 

x 0 = 0. 

Dalla (4) segue: 

x (0) = − Aω sin ϕ = 0 ⇔ ϕ = 0 

(6) 

x(0) = Acos(0) = x ⇔ A= x 

(7) 

0 0 

( ω ) 

x() t = x cos t 

(8) 

0 0 

( ) 

x() t =−ω 

x cosωt 

(9) 

2 

0 0 0 

Oscillatore Armonico - Risonanza - 1


Dalla (10) si vede che il sistema ha una pulsazione propria, 0 

questa pulsazione corrispondono la frequenza 

1 

2 m 

T = = π 

ν k 

0 

L'energia potenziale del sistema è data da 

− k+ ω m= 

0 

(10) 

2 

0 

ν 

ω , data da 0 

ω 1 

2π 2π 

k 

m 

k 

ω = . A 

m 

0 

0 = = e il periodo 

1 2 1 2 1 2 2 

U = kx = k⎡x0cos( ωt) ≡ kx0 cos ( ωt) 

2 2 

⎣ ⎤⎦ 

(11) 

2 

mentre l'energia cinetica, utilizzando le (4), (6) e (7) è data da 

1 2 1 2 1 2 2 2 

T = mx = m⎡− x0ω0sin ( ω0t) ⎤ = mω0x0 sin ( ω0t) 

2 2 

⎣ ⎦ 

(12) 

2 

2 

Dalla (10) ricaviamo k = mω, 

col che la (12) si può riscrivere: 

0 

1 2 2 

T = kx0 sin ( ω0t) 

(13) 

2 

Utilizzando la (11) e la (13) si vede che la somma delle energie cinetica e potenziale è 

1 2 2 1 2 2 1 2 

E = T + U = kx0 sin ( ωt) + kx0 cos ( ωt) 

= kx0 ∀ t (14) 

2 2 2 


xo 


x 

 

v 

0 A 

0 A 

 

v 

1 

 

v 2 

0 A 

0 A 

1 2 3 4 5 6 7 8 

3 

4 

x 

x 

x 

x 

-A 

-A 

0 A 

0 A 

Oscillatore Armonico - Risonanza - 3 

5 

 

v 6 

t 

 

v 

E=T+U 

7 

0 A 

 

v 8 

0 A 

1 2 2 

U = kx cos ωt 

= U 

2 0 

max 

1 2 2 

T = kx sin ωt 

= T 

2 0 

max 

t 

⎡ 

⎣⎢ 

⎡ 

⎣⎢ 

x 

x 

x 

x 

1+ cos 2ωt 

2 

1−cos 2ωt 

2 

⎤ 

⎦⎥ 

⎤ 

⎦⎥


2 Oscillazioni smorzate 

Se sul sistema agisce anche una forza resistente che dipende dalla velocità (resistenza 

 

di tipo viscoso) f =−bv 

, si ha 

− kxi 

 

N 

mg 

la cui proiezione sull'asse x fornisce 

f 

x 

kxiˆ 

− − bv + mg + R = ma (15) 

mx = −kx−bx ⇒ mx + bx + kx = 0 

(16) 

che è un'equazione differenziale lineare a coefficienti costanti. Cerchiamo soluzioni 

del tipo 

Sostituendo nella (16) si ha: 

γ t 

Essendo e > 0 ∀ t , deve quindi essere 

x = e ⇒ x = γe ⇒ x= γ e 

γ t γt 2 γt 

2 ( γ γ ) 

γ t 

e m + b + k = 0 

(17) 

2 

mγ bγ k 

ovvero γ deve essere soluzione della (18), e sarà quindi dato da 

+ + = 0 

(18) 

b 

2 

b k 

1,2 2 

Si hanno tre diversi casi a seconda che sia il discriminante 

1. Se 0 

∆> (grandi smorzamenti), γ 1 e 2 

soluzione dell'equazione del moto è 

γ = − ± − (19) 

2m 4m 

m 

2 

⎛ b ⎞ k > 

∆= ⎜ ⎟ − 0 

⎝2m⎠ m < 

γ sono reali e distinte, e negative. La 

∆ ∆ 

( ) 

b 

− t 

γ1t γ2t 

2m 

t t 

1 2 1 2 

xt () = Ae + Ae = e Ae + Ae (20) 



2. Se ∆= 0 (smorzamento critico), γ 1 e γ 2 sono reali e coincidenti, e si ha 

b 

γ1 = γ2 

=− . La soluzione dell'equazione del moto è 

2m 

b 

− t 

2m 

( ) 

x() t = e A + At 

(21) 

1 2 

3. Se ∆< 0 (piccoli smorzamenti), γ 1 e γ 2 sono immaginarie; si ha 

b 

γ1,2 =− ± iω 

', 

con i = 

2m 

− 1 e ω ' = 

k ⎛ b ⎞ 

−⎜ ⎟ 

m ⎝2m⎠ (22) 

La soluzione dell'equazione del moto è: 

Sfruttando le formule di Eulero 

si ottiene 

b 

− t 

2m 

iω't −iω't 

( 1 2 ) 

xt () = e Ae + Ae 

(23) 

iθ 

− iθ 

e = cos θ + i sin θ ; e = cos θ − i sin θ 

b 

− t 

2m 

( ) 1 cos ' sin ' 2 cos ' sin ' 

( ω ω ) ( ω ω ) 

x t = e ⎡⎣A t+ i t + A t+ i t ⎤⎦ 

= 

Poniamo ora A1 A2 Acosϕ da cui 

b 

− t 

2m 

⎡⎣ ( 1 2) cos ω ' ( 1 2) 

sin ω'⎤⎦ 

(24) 

= e A + A t + i A − A t 

+ = e ( ) 

i A − A = A ϕ ; si ha 

1 2 sin 

b 

− t 

2m 

( ) cos ' cos sin ' sin 

[ ω ϕ ω ϕ] 

xt = Ae t + t 

(25) 

b 

− t 

2m 

() cos ' 

Queste sono oscillazioni smorzate con pulsazione 

( ω ϕ) 

xt = Ae t+ 

(26) 

k ⎛ b ⎞ k 

ω ' = − ⎜ ⎟ < = ω0 

m ⎝2m⎠ m 

2 

Oscillatore Armonico - Risonanza - 5 

2 

(27)


3 Oscillazioni forzate e Risonanza 

Se oltre alla forza elastica di richiamo ed alla resistenza di tipo viscoso c'è anche 

un'altra forza di tipo alternativo espressa da ( ) ˆ 

 

F = Fcos ωt 

i , il 2° principio della 

dinamica si scrive come 

N 

F 

 

f 

= F cos (ωt) î 

− kxi ˆ 

mg 

che proiettata sull'asse x da 

x 

La figura [D.Sette, Lezioni di Fisica, Ed. 

Veschi] rappresenta la funzione x(t) per un 

oscillatore smorzato. Le curve II e III 

rappresentano due possibili risposte nel caso 

∆ >0 (grandi smorzamenti); la curva IV 

rapprenta il caso ∆=0 (smorzamento critico), 

mentre la curva I rappresenta il caso ∆


più un integrale particolare della equazione completa (29). L'integrale generale della 

(30) si risolve come descritto al punto 2), e rappresenta il comportamento transitorio 

(o transiente) del sistema dopo che viene perturbato. A tempi lunghi questa 

comportamento smorzato scompare, e la soluzione della (29) la cerchiamo nella forma 

che ha derivate 

( ω ϕ ) 

xt () = X cos t− 

(31) 

m 

( ) 

xt () = −ωX sinωt−ϕ 

(32) 

m 

2 

() m cos 

( ) 

xt = −ωX ωt−ϕ (33) 

Sostituendo le (31), (32) e (33) nella (29) si ottiene la seguente equazione: 

( ) ( ) ( ) ( ) 

− − − − + − = 

2 

mωXmcos ωt ϕ bωXmsinωt ϕ kXmcosωt ϕ Fcos ωt 

Usando le formule trigonometriche di sottrazione, si ottiene: 

( cos cos sin sin ) ( sin cos cos sin ) 

− ω ω ϕ+ ω ϕ − ω ω ϕ− ω ϕ + 

2 

m Xm t t b Xm t t 

raccogliendo e quindi separando i termini in cos( t) 

m 

( cosω cosϕ sinω sinϕ) cos( 

ω ) 

+ kX t + t = F t 

ω e sin ( t) 

( 2 

mω Xmcosϕ bωXmsinϕ kXmcosϕ F) cosωt 

( 2 

m m m ) 

− + + − + 

ω si ottiene quindi: 

+ −mω X sinϕ− bωX cosϕ+ kX sinϕ sinωt = 0 

Si dividono ora tutti i termini per m, e ricordando che 

km= ω si impone che la 

precedente equazione sia sempre soddisfatta, il che implica che entrambe la parentesi 

devono separatamente essere uguali a 0; si ottiene il seguente sistema di equazioni 

ovvero 

2 bω2 F 

− ω Xmcosϕ+ Xmsinϕ+ ω0Xmcosϕ = 

m m 

2 bω 

2 

−ω Xmsinϕ− Xmcosϕ+ ω0Xmsinϕ = 0 

m 

⎧ 2 2 

bωF ( ω0− ω ) Xmcosϕ+ Xmsinϕ 

= 

⎪ 

m m 

⎨ 

⎪ 2 2 bω 

( ω0−ω ) Xmsinϕ− Xmcosϕ 

= 0 

⎪⎩ 

m 

e le costanti X m e ϕ soddisfano quindi le relazioni 

2 

0 



X 

X 

m 

m 

cos 

sin 

( ϕ ) 

( ϕ ) 

dalle quali si ottiene, quadrando e sommando: 

mentre, dividendo la (35) per la (34): 

X 

Dalle (36) e (37) si ha che: 

m 

= 

F 

( ) 2 

0 

2 2 

Fm( 

ω0−ω ) 

( 0 − 

2 

) + 

= 

2 

m 

2 

ω 

2 

ω 

2 2 

b ω 

= 

Fbω 

2 

m 

2 2 

ω − ω 

2 2 

+ b ω 

2 2 2 2 2 

m ω − ω + b ω 

tgϕ 

= 

bω 

2 2 ( ω0−ω ) 

( ) 2 

0 

1. lo spostamento della massa m è sfasato di un angolo ϕ rispetto alla forza F ; 

2. l'angolo di sfasamento è sempre positivo, e varia tra 0 e π ; 

3. l'ampiezza di oscillazione X m dipende da ω ; 

4. il massimo valore di X m si ha per ω = ω0 1−( b 2mω)2≅ 

ω0 

(frequenza di 

risonanza); in corrispondenza a tale valore di frequenza lo sfasamento vale 

ϕ = π 2. 

m 

(34) 

(35) 

(36) 

(37)

1 Oscillazioni libere (oscillatore armonico) ( ) ( ) ( ) ( ) 0 e ( )0 - Fisica

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?